Memorylessness and Entropy « Myself, Coding, Ranting, and Madness

Memorylessness and Entropy

13 Aug 2012 8:00 Tags: None

Any one who has delved into probability or stochastic will have come across the idea of a Markovian system1: one where each new state or value is dependent on the one that immediately precedes it. However, this is generally only ever examined in the contexts where it is known that the property holds, or that accepting the property is a valid approximation.

What I'd like to discuss today is what can happen if you examine a process with a limited amount of memory without out any knowledge of its properties, and the conclusions that follows, concluding with the similarities between finding models .

Consider then the time-variant random variable X, which is defined as: $\begin{array}{l} X_t \in \{0, 1\}, t \ge 0 \\ X_t = \left\{ \begin{array}{ll} 1 - X_{t-2} & t \textrm{ even} \\ 1 & t \textrm{ odd, with probability 0.5} \\ 0 & t \textrm{ odd, with probability 0.5} \end{array} \right. \end{array}$

This process, although contrived, has some interesting properties. Firstly, it is wide-sense stationary2 3. It does, however, clearly have some form of memory as every other item follows a high-low pattern.

However, the state space is only defined as a single bit. If we do the analysis considering it as such, either analytically4, or by looking at samples, an entirely different pattern emerges.

$\begin{array}{l} \textrm{Let } X' \textrm{ be the new state.} \\ \textrm{Let } X \textrm{ be the current state.} \\ \\ \textrm{If } X' \textrm{ is an odd state:} \\ \mathbb{P} \left( X' = 0 | X = 0 \right) = \mathbb{P} \left( X' = 0 | X = 1 \right) = \\ \mathbb{P} \left( X' = 1 | X = 0 \right) = \mathbb{P} \left( X' = 1 | X = 1 \right) = 0.5 \\< \\ \textrm{ By <law allowing combination of conditional probabilities>: } \\ \mathbb{P} \left( X' = 0 \right) = \mathbb{P} \left( X' = 1 \right) = 0.5 \\ \\ \textrm{If } X' \textrm{ is an even state, and } X'' \textrm{ is the previous even state:} \\ \mathbb{P} \left( X' = 0 | X = 0 \right) = \mathbb{P} \left( X = 0 | X'' = 1 \right) = 0.5 \\ \\ \textrm{By symmetry, we conclude that in all cases:} \\ \mathbb{P} \left( X' = 0 \right) = \mathbb{P} \left( X' = 1 \right) = 0.5 \end{array}$

This gives us the state transition below, and a process that does not only satisfy the Markovian property, but is entirely memoryless.

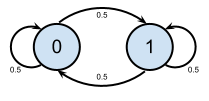
From here on, thing get even better. The process described has gone from wide-sense stationary to being a truly stationary process5. Analytically, it also carries no redundant information — the standard test of bitwise Shannon entropy6 yields the following:

$H = - \sum\limits_{i=0}^1 \mathbb{P} \left(X = i\right) \log_2(\mathbb{P} \left(X = i\right)) = -2 * 0.5 \, \log_2(0.5) = 1 \textrm{ bit/bit}$

So, the overall information content is the same as the length of the transmission.

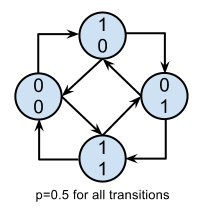
If we redo the analysis, this time taking: $Y_t = 2 * X_{2t} + X_{2t+1}$ giving the values of Y in the range 0 to 3. The state transition diagram is shown (derivation omitted). In this case, the system has four states with equal probability over the duration of a sample, still giving a Shannon entropy of 1bit/bit. However, the transition is now dependent on the current state, so we're back to the standard definition of the Markovian property.

We can do it again taking four consecutive values. As we know that the first and third values must be opposite and consistent across each sample, we find that only four of the sixteen available states will occur7. The second and fourth values are truly random, and there is no dependence between the four-bit blocks. Thus we would arrive at state diagram where each of the four nodes is connected to all of the nodes, including itself.

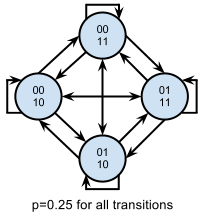
This system is back to being entirely memoryless, but now has a lower information efficiency. The Shannon entropy is then calculated as: $\begin{array}{l} \textrm{Let }Z\textrm{ be the process described, that can reach the states } v = \left\{0010, 0011, 0110, 0111\right\}\\ \\ H = - \sum\limits_{i \in v} \mathbb{P} \left(Z = i\right) \log_{16}(\mathbb{P} \left(Z = i\right)) = -4 \times 0.25 \, \log_{16}(0.25) = 0.5 \textrm{ bits/bit} \end{array}$ This is what one would expect when half of the bits are fixed.

If we were then to take n*4-bit samples, we'd be able to reach any combination of the 4-bit patterns repeated n times, giving 4ⁿ possibilities of equal probability, out of 16ⁿ possible values. This allows us to derive a general case entropy: $H = - \sum\limits_{i = 1}^{4^n} 4^{-n} \ln(4^{-n}) / \ln(16^n) = -4^{n} 4^{-n} \frac{-n \ln(4)}{2n \ln(4)} = 0.5 \textrm{ bits/bit}$

Using this, we can plot a chart of the apparent entropy against the word size, allowing us to get a hint at the underlying pattern. We could augment this by looking at the other possibly values, those which are not powers of 2. Those of you with an interest in cryptography will have realised this is a slow replication of a Kasiski examination8 style of analysis on a Vigenère cipher9. This, I suppose, underlies the problem with attempting to model unknown systems: they are, in man respects, a cipher for reality.

1 ↑ http://en.wikipedia.org/wiki/Markov_property
2 ↑ http://en.wikipedia.org/wiki/Stationary_process#Weak_or_wide-sense_stationarity
3 ↑ The mean is a constant (0.5) and the auto correlation function depends only on the distance between the two samples.
4 ↑ Which is somewhat stupid as we're knowingly removing data.
5 ↑ http://en.wikipedia.org/wiki/Stationary_process#Weak_or_wide-sense_stationarity
6 ↑ http://en.wikipedia.org/wiki/Entropy_(information_theory)#Definition
7 ↑ That the first value is 0 is not an assumption, as we may simply define however the very fist bit is encoded as the representation of 0 in this system.
8 ↑ http://en.wikipedia.org/wiki/Kasiski_examination
9 ↑ http://en.wikipedia.org/wiki/Vigen%C3%A8re_cipher

Myself, Coding, Ranting, and Madness

Home

Feeds

Tags

Other

Memorylessness and Entropy