The LaTeX Atrocities: Dealing with Numbers
LaTeX has quite possibly the strangest learning curve I have ever encountered in my time with languages of all kinds. This is, of course, because it is not really intended to be a language which you extend, but merely use. This is reflected in all the documentation which you can find with ease on the internet: it leads you through the different common type setting tasks, and perhaps briefly mentions the possibility of defining your own commands right at the end. What seems to be consistently lacking is any input on what is considered good practice for your own commands.
This occurs, I believe, because it's assumed anyone who really wants to mess around with changing things will do some research in TeX, the underlying tool, and go from there.
I, on the other hand, feel it means a lot of stuff ends up entirely undocumented. So, I thought I write about some of the things I've learnt, whether by accident, experimentation, or doggedly searching the internet.
Numbers Types in (La)TeX.
Clearly, at some level, LaTeX does a lot of numerical processing. If nothing else, at some point it has to deal with things like margins and wrapping text. Like most features of LaTeX, this is also available to the user.
The internal TeX registers can hold different of kinds of number-like data (dimensions, counters, etc.). The main number register appears to be, however, limited to integers1
The \the Operator
To put it simply, the \the macro takes a register definition, and converts the value to a string that will be typeset. The fact it's needed actually shows up that TeX has some underlying concept of types other than strings, a fact that is often overlooked. Stack Exchange / Tex has an excellent explanation of its function in detail2
Basic use of \numexpr
\numexpr creates, on the stack, a number register based on the expression that follows it. The operation is designed to have no side effects3, and supports the basic operations (addition, subtraction, multiplication and division).

The selected expression will continue being processed until something forces \scanint, the underlying macro for finding inputs that can be understood as integers, to return an empty value without causing an error. The best method for doing this is to use the \relax command, which outputs no value, but is taken as the end of the current expression
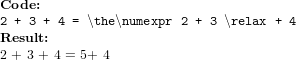
Expression Processing
The expression is handled according to the age-old rules of arithmetic.
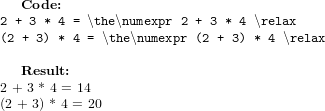
The underlying type being used is still, however, limited to being an integer. The fourth tests shows, however, that a non-integer value can be recognised as some kind of number format, even if it can not be processed as one. This leads to the odd situation where an expression will not cause an error, but will not be expanded correctly. Adding in a non-numeric string causes an error, regardless of ordering4
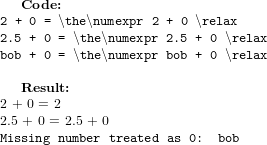
Floating Point Handling
As we have already seen, \numexpr doesn't like handling non-integer inputs. However, the division operator is implemented, and is functional. Values are rounded to the nearest integer.

Other Packages
LaTeX allows for a large upgrade of the default handling through the calc package5. This extends the other number-like controls for counters and dimensions, and adds a floating-point layer, with non-integers being defined with \real{value} or \ratio{numerator}{denominator}.
Floating point values are available through the fp package6, the documentation for which is nearly non-existent. However, it appears to use a fixed-point data type, and the \FPupn macro implements an expression system that is quite powerful, and uses postfix operators for extra hipster-ism.

- 1 ↑ This is shown in more detail in examples 4–6
- 2 ↑ http://tex.stackexchange.com/questions/38674/the-the-command
- 3 ↑ http://www-sop.inria.fr/marelle/tralics/doc-n.html#cmd-numexpr
- 4 ↑ The example of "0 + bob" is not shown, but has the same result
- 5 ↑ http://tug.org/texlive/Contents/live/texmf-dist/doc/latex/tools/calc.pdf
- 6 ↑ http://www.ctan.org/tex-archive/macros/latex/contrib/fp/